强化学习入门

摘要

强化学习（Reinforcement Learning）是目前机器学习领域一个比较热门的研究方向。这篇报告主要介绍强化学习的基本概念和算法。

强化学习基本概念

强化学习

强化学习是机器学习领域的一类学习问题，它与常见的有监督学习、无监督学习等的最大不同之处在于，它是通过与环境之间的交互和反馈来学习的。正如一个新生的婴儿一样，它通过哭闹、吮吸、爬走等来对环境进行探索，并且慢慢地积累起对于环境的感知，从而一步步学习到环境的特性使得自己的行动能够尽快达成自己的愿望。再比如，这也同我们学习下围棋的模式类似，我们通过和不同的对手一盘一盘得对弈，慢慢积累起来我们对于每一步落子的判断，从而慢慢地提高自身的围棋水平。由DeepMind研发的AlphaGo围棋程序在训练学习的过程中就用到了强化学习的技术。

下面让我们来正式地定义一下强化学习问题。强化学习的基本模型就是个体-环境的交互。个体（agent）就是能够采取一系列行动并且期望获得较高收益或者达到某一目标的部分，比如我们前面例子中的新生婴儿或者在学习下围棋的玩家。而与此相关的另外的部分我们都统一称作环境（environment），比如前面例子中的婴儿的环境（比如包括其周围的房间以及婴儿的父母等）或者是你面前的棋盘以及对手。整个过程将其离散化为不同的时刻（time step）。在每个时刻环境和个体都会产生相应的交互。个体可以采取一定的行动（action），这样的行动是施加在环境中的。环境在接受到个体的行动之后，会反馈给个体环境目前的状态（state）以及由于上一个行动而产生的奖励（reward）。其中值得注意的一点是，这样个体-环境的划分并不一定是按照实体的临近关系划分，比如在动物行为学上，动物获得的奖励其实可能来自于其自身大脑中的化学物质的分泌，因此这时动物大脑中实现这一奖励机制的部分，也应该被划分为环境；而个体就仅仅只包括接受信号并且做出决定的部分。

上面所描述的个体-环境相互作用可以使用图一中的示意图表示。存在一连串的时刻$t=1, 2, 3 \cdots$，在每一个时刻中，个体都会接受到环境的一个状态信号$S_t \in \mathcal{S}$，在每一步中个体会从该状态允许的行动集中挑选一个来采取行动$A_t \in \mathcal{A}(S_t)$，环境接受到这个行动信号之后，在下一个时刻环境会反馈给个体相应的状态信号$S_{t+1} \in \mathcal{S}^+$和即时奖励$R_{t+1}\in \mathcal{R} \subset \mathbb{R}$。其中，我们把所有的状态记做$\mathcal{S}^+$，把非终止状态记做$\mathcal{S}$。

图一：个体环境相互作用

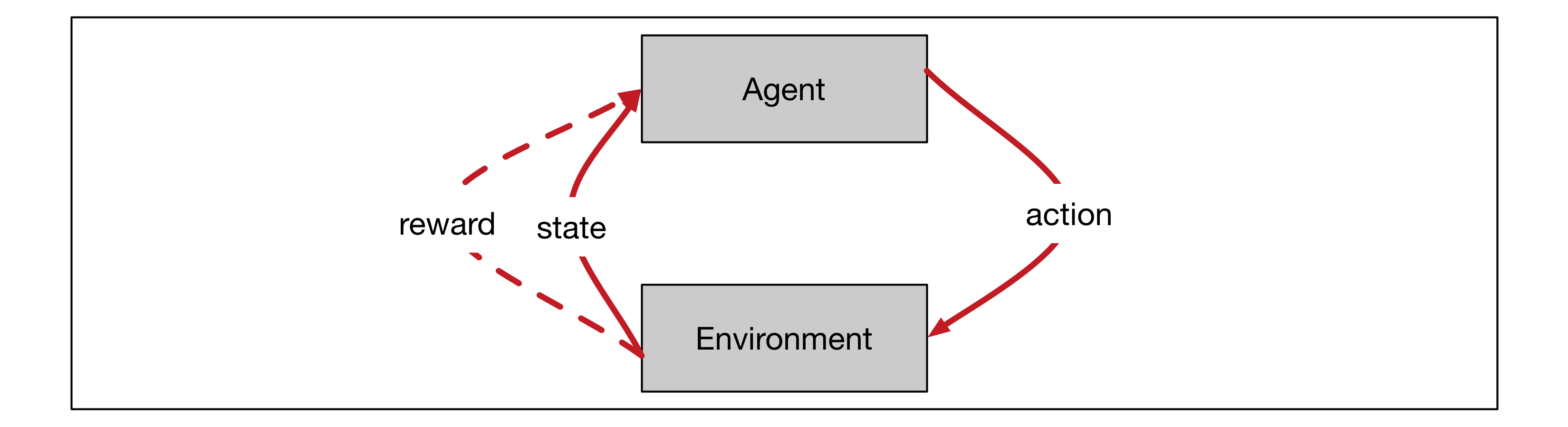
强化学习的目标是希望个体从环境中获得的总奖励最大，即我们的目标不是短期的某一步行动之后获得最大的奖励，而是希望长期地获得更多的奖励。比如一个婴儿可能短期的偷吃了零食，获得了身体上的愉悦（即，获取了较大的短期奖励），但是这一行为可能再某一段时间之后会导致父母的批评，从而降低了长期来的总奖励。在很多常见的任务中，比如下围棋，在一局棋未结束的时候奖励常常都是为零的，而仅当棋局结束的那一个时刻才会根据个体的输赢产生一个奖励值；而在有些任务中，环境给予奖励可能分布在几乎每个时刻中。对于像下围棋这样存在一个终止状态，并且所有的奖励会在这个终止状态及其之前结算清的任务我们称之为回合制任务（episodic task）；还存在另外的一类任务，它们并不存在一个终止状态，即原则上它们可以永久地运行下去，这类任务的奖励是分散地分布在这个连续的一连串的时刻中的，我们称这一类任务为连续任务（continuing task）。由于我们的目标是希望获得的总奖励最大，因此我们希望量化地定义这个总奖励，这里我们称之为收益（return）。对于回合制任务而言，我们可以很直接定义收益为

\[G_t = R_{t+1} + R_{t+2} + \cdots + R_T\]

其中$T$为回合结束的时刻，即$S_T$属于终止状态。对于连续任务而言，不存在一个这样的终止状态，因此，这样的定义可能会在连续任务中发散。因此我们引入另外一种收益的计算方式，称之为衰减收益（discounted return）。

\[G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}\]

其中衰减率$\gamma$满足$0 \le \gamma \le 1$。

如果我们可以计算出每个状态或者采取某个行动之后收益，那么我们每次行动就只需要采取收益较大的行动或者采取能够到达收益较大状态的行动。这也是强化学习中的一个核心问题，即如何估计某个状态或者行动产生的收益。

强化学习的结果是一个策略（policy），这个策略给出了在每个状态下我们应该采取的行动，我们可以把这个策略记做 $\pi (a| s)$ ，它表示在状态$s$下采取行动a的概率。通常，强化学习通过对于和环境的交互，逐步准确地估计出相应的收益，同时逐渐收敛到一个好的策略上。

马可夫决策过程

上述定义中的环境可能是确定性，也可能是概率性的，不管是哪种情况，我们这里暂时假定我们面对的环境是相对稳定的（stationary），即存在以下概率

\[Pr\{S_{t+1} = s', R_{t+1} = r | S_0, A_0, S_1, A_1, \cdots, S_t, A_t\}\]

其中$S_0, A_0, S_1, A_1, \cdots, S_t, A_t$是当前状态之前个体所经历的一系列状态和行动。我们可以注意到，这一概率如果存在，那么它完全描述了我们在强化学习中所需要的关于环境的所有信息。我们再假定它满足马可夫性，即

\[p(s', r| s, a) = Pr\{S_{t+1} = s', R_{t+1} = r | S_t, A_t\} = Pr\{S_{t+1} = s', R_{t+1} = r | S_0, A_0, S_1, A_1, \cdots, S_t, A_t\}\]

我们注意到，这一的假设使得我们可以仅仅利用当前状态来估计接下来的收益，即仅仅使用当前状态来估计的策略并不比使用所有历史的策略差。可以说马可夫性带给我们了极大的计算上的便利，我们不用每一步都去处理所有的历史步骤，而是只需要面对当前的状态来进行处理。同时注意到，可能有些信息并没有被完整的包含到模型的状态信号$S_t$中，这使得模型并不满足马可夫性。不过我们一般还是认为它们是近似地满足马可夫性的，因此仅仅使用当前状态的信息来做出对于未来收益的预测和行动的选择并不是很差的策略。

满足上述马可夫性的强化学习任务，我们称之为马可夫决策过程（Markov dicision process, MDP）。如果状态空间$\mathcal{S}^+$和行动空间$\mathcal{A}(S), \forall S \in \mathcal{S}$都是有限的，我们称之为有限状态的马可夫决策过程（finite MDP）。接下来，我们将基于马可夫性推导出强化学习领域最核心的Bellman方程。

首先，我们可以做如下定义。定义马可夫决策过程的动力学特征

\[p(s', r|s, a) = Pr\{S_{t+1}=s', R_{t+1} = r | S_t = s, A_t = a\}\]

当我们知道了马可夫决策过程的动力学特征之后，我们就能对环境进行模拟，给出以下诸多物理量，比如在状态$s$下采取行动$a$的期望收益

\[r(s, a) = \mathbb{E}[R_{t+1} | S_t = s, A_t = a] = \sum_{r\in\mathcal{R}} r \sum_{s'\in\mathcal{S}} p(s', r | s, a)\]

状态转移概率

\[p(s'|s, a) = Pr\{S_{t+1}=s'| S_t = s, A_t = a\} = \sum_{r\in\mathcal{R}} p(s', r | s, a)\]

状态$s$下采取行动$a$并且到达状态$s’$之后的期望收益

\[r(s, a, s') = \mathbb{E}[R_{t+1} | S_t = s, A_t = a, S_{t+1}=s'] = \dfrac{\sum_{r\in\mathcal{R}}r p(s', r|s, a)}{p(s'|s, a)}\]

接下来我们引入强化学习领域常用的两个函数状态价值函数（state value function）$v_\pi(s)$和行动价值函数（action value function）$q_\pi(s, a)$，其中函数$v_\pi(s)$表示的是当到达某个状态$s$之后，如果接下来一直按着策略$\pi$来行动，能够获得的期望收益；函数$q_\pi(s, a)$表示的是当达到某个状态$s$之后，如果采取行动$a$，接下来再按照策略$\pi$来行动，能获得的期望收益。它们的具体定义如下。

\[v_\pi(s) = \mathbb{E}_\pi[G_t | S_t = s] = \mathbb{E}[\sum_{k=0}^\infty \gamma^k R_{t+k+1} | S_t = s]\] \[q_\pi(s, a) = \mathbb{E}_\pi [G_t | S_t = s, A_t = a] = \mathbb{E}[\sum_{k=0}^\infty \gamma^k R_{t+k+1} | S_t = s, A_t = a]\]

递归地展开上面这两个公式即可得到相应的两个Bellman方程，比如对于上述关于$v_\pi(s)$的式子，有

\[\begin{aligned} v_\pi(s) & = \mathbb{E}_\pi[\sum_{k=0}^\infty \gamma^k R_{t+k+1} | S_t = s]\\ &= \mathbb{E}_\pi[R_{t+1} + \gamma \sum_{k=0}^\infty \gamma^k R_{t+k+2} | S_t = s] \\ &= \sum_a \pi(a|s) \sum_{s'} \sum_r p(s', r|s, a) [r + \gamma \mathbb{E}_\pi[\sum_{k=0}^\infty \gamma^k R_{t+k+2} | S_{t+1} = s']] \\ &= \sum_a \pi(a|s) \sum_{s'} \sum_r p(s', r|s, a) [r + \gamma v_\pi(s')] \\ & \forall s \in \mathcal{S} \end{aligned}\]

这就是关于状态价值函数的Bellman方程，它描述的是当前状态的价值函数和它后续状态价值函数之间的递归关系。同理可以得到关于行动价值函数的Bellman方程。

那么对于一个有限状态的马可夫决策过程来说，是否存在一个最优的策略呢？如果一个策略$\pi’$在任何状态$s \in \mathcal{S}$下都有$v_{\pi’}(s) \le v_{\pi}(s)$，那么我们称策略$\pi’$优于$\pi$。对于所有的策略排序，我们总可以找到最优策略（有可能不止一个最优策略），我们记最优策略为$\pi_*$，最优策略具有如下性质

\[\begin{aligned} v_*(s) &= \max_\pi v_\pi(s) \\ q_*(s, a) &= \max_\pi q_\pi(s, a) \end{aligned}\]

使用上述类似的方法，我们可以得到最优情况下的Bellman方程（Bellman optimality equation）

\[\begin{aligned} v_*(s) &= \max_{a\in\mathcal{A}(s)} \sum_{s', r} p(s', r|s, a)[r + \gamma v_*(s')] \\ q_*(s, a) &= \sum_{s', r} p(s', r|s, a) [r + \gamma \max_{a'} q_*(s', a')] \end{aligned}\]

若干基本的强化学习算法

有了上述的模型抽象之后，我们在这里介绍几种基础的强化学习算法：动态规划（dynamic programming, DP）、蒙特卡洛方法（Monte Carlo methods， MC）和时间差分方法（temporal-difference， TD）。最后我们将会介绍TD($\lambda$)算法，是对于以上几种方法的统一。

动态规划方法

这里先给出动态规划算法

\[\begin{aligned} & \text{算法一：Dynamic Programming} \\ 1\quad & \text{initialize array V arbitrarily (eg. } V(s)=0, \forall s \in \mathcal{S}^+ \text{)} \\ 2\quad & \text{repeat} \\ 3\quad & \quad \Delta \leftarrow 0 \\ 4\quad & \quad \text{for each } s \in \mathcal{S} \\ 5\quad & \quad \quad v \leftarrow V(s) \\ 6\quad & \quad \quad V(s) \leftarrow \max_a \sum_{s', r} p(s', r|s, a)[r + \gamma V(s')] \\ 7\quad & \quad \quad \Delta \leftarrow \max(\Delta, |v - V(s)|) \\ 8\quad & \text{until } \Delta < \theta \text{ (a small positive number)} \\ 9\quad & \text{output a deterministic policy, } \pi \approx \pi_* \text{, such that} \\ 10\quad & \pi(s) = arg\max_a \sum_{s', r} p(s', r|s, a)[r + \gamma V(s')] \end{aligned}\]

动态规划算法其实质是把前面推导的Bellman方程化为了增量的形式进行计算，当算法收敛到不动点的时候，这时得到的状态价值函数就满足最优情形下的Bellman方程，对应的贪心策略就是最优策略。其中，核心的算法在第6行，它迭代地将状态价值函数$V(s)$逼近最优状态价值函数$v_*(s)$。算法的循环中没有显式地定义每一步对应的策略，我们可以对于每一步迭代的价值函数$V(s)$都定义相应的贪心策略。利用以下定理，我们可以知道，经历每一步的迭代，之后策略都不比之前的策略差；从而当算法收敛的时候，我们可以得到最优策略。

Policy Improvement Theorem

如果存在一对确定性的策略$\pi$和$\pi’$，使得$q_\pi(s, \pi’) \ge v_\pi (s), \forall s \in \mathcal{S}$，那么$\pi’$不比$\pi$差。

如果存在一对确定性的策略$\pi$和$\pi’$，使得$v_\pi’(s) \ge v_\pi (s), \forall s \in \mathcal{S}$，那么$\pi’$不比$\pi$差。

上述算法的第6行中可以看到，$V(s)$是单调不减的，因此，其对应的策略也应该是单调提升的。

从第5行-第7行可以看出，在每一轮迭代中，都需要对于状态空间中所有的状态访问一次。当状态空间庞大的时候，这样的循环会十分消耗时间。可以采用异步DP的算法，每轮迭代仅更新一部分的状态，只要保证在多轮迭代中，每个状态都能被访问到，这样的异步DP算法一样能收敛到最优策略上。

DP算法对于每一个状态价值函数的估算都需要知道其后一步状态所有状态的收益估计值，这种特征我们称之为full backup。同时我们注意到，在DP算法中，我们认为反映环境的所有信息$p(s’, r|s, a)$是已知的，即我们已经拥有了对于环境的建模，这种利用反映环境信息的模型来进行计算的方法我们称之为model-based method。从某种意义上来说，DP方法本质上还并没有涉及到对于环境的“学习”过程，因为DP没有通过与环境的交互来获取关于环境的信息。

蒙特卡洛方法

蒙特卡洛方法的主要思想是随机地从一些状态出发，然后按照行动策略（behavior policy）$\mu$采取行动，直到达到终止状态，然后回溯地利用探索到的这部分信息来更新目标策略（target policy）$\pi$下的价值函数。其中，行动策略和目标策略在每一轮迭代中也通常是与当前的价值函数相关的。因此此类方法也使用了与上述DP方法类似的思想，即在每轮迭代中交替地进行对于当前策略价值函数的估计（policy evaluation）和基于当前价值函数改进策略（policy improvement），这样的算法框架我们称之为广义的策略循环（gerneralized policy iteration）。这样的框架在强化学习很多算法里面都会使用到。

当每一轮的行动策略与目标策略一致的时候，我们称这样的方法为on-policy的；反之，我们称之为off-policy的。对于这两种算法，这里都给出相应的算法框图。

\[\begin{aligned} & \text{算法二：Monte Carlo Method (on-policy)} \\ 1\quad & \text{initialize } \forall s \in \mathcal{S}, a \in \mathcal{A}(s)\\ 2\quad & \quad Q(s, a) \leftarrow \text{arbitrary} \\ 3\quad & \quad Returns(s, a) \leftarrow \text{empty list} \\ 4\quad & \quad \pi(a|s) \leftarrow \text{arbitrary }\epsilon\text{-soft policy} \\ 5\quad & \text{repeat forever:} \\ 6\quad & \quad \text{generate an episode using }\pi \\ 7\quad & \quad \text{for each pair } s, a \text{ in the episode:} \\ 8\quad & \quad \quad G \leftarrow \text{return following the first occurance of } s, a \\ 9\quad & \quad \quad \text{append } G \text{ to } Returns(s, a) \\ 10\quad & \quad \quad Q(s, a) \leftarrow \text{average}(Returns(s, a)) \\ 11\quad & \quad \text{for each } s \text{ in the episode:} \\ 12\quad & \quad \quad A^* \leftarrow arg\max_a Q(s,a) \\ 13\quad & \quad \quad \text{for all } a\in\mathcal{A}(s) \\ 14\quad & \quad \quad \quad \pi(a|s) \leftarrow \begin{cases} 1-\epsilon+\epsilon/|\mathcal{A}(s)| & \text{if } a = A^* \\ \epsilon/|\mathcal{A}(s)| & \text{if } a \neq A^* \end{cases} \end{aligned}\] \[\begin{aligned} & \text{算法三：Monte Carlo Method (off-policy)} \\ 1\quad & \text{initialize } \forall s \in \mathcal{S}, a \in \mathcal{A}(s)\\ 2\quad & \quad Q(s, a) \leftarrow \text{arbitrary} \\ 3\quad & \quad C(s, a) \leftarrow 0 \\ 4\quad & \quad \pi(s) \leftarrow \text{a deterministic policy that is greedy w.r.t.} Q\\ 5\quad & \text{repeat forever:} \\ 6\quad & \quad \text{generate an episode using any soft policy }\mu \\ 7\quad & \quad \quad S_0, A_0, R_1, \cdots, S_{T-1}, A_{T-1}, R_T, S_T \\ 8\quad & \quad G \leftarrow 0 \\ 9\quad & \quad W \leftarrow 1 \\ 10\quad & \quad \text{for } t = T-1, T-2, \cdots, \text{ downto } 0 \text{:} \\ 11\quad & \quad \quad G \leftarrow \gamma G + R_{t+1} \\ 12\quad & \quad \quad C(S_t, A_t) \leftarrow C(S_t, A_t) + W \\ 13\quad & \quad \quad Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \frac{W}{C(S_t, A_t)} (G - Q(S_t, A_t)) \\ 14\quad & \quad \quad \pi(S_t) \leftarrow arg\max_a Q(S_t, a) \\ 15\quad & \quad \quad \text{if } A_t \neq \pi(S_t) \text{ then exit forloop} \\ 16\quad & \quad \quad W \leftarrow W / \mu(A_t|S_t) \\ \end{aligned}\]

对于MC方法，只有满足如下两个条件的时候才能够保证算法收敛到最优策略

• 当循环次数趋向无穷的时候，每个状态被遍历的次数也趋向无穷
• 主循环被执行无穷多次

对于第二点，我们只能在资源允许的情况下尽可能多地运行主循环。对于第一点来说，我们的解决方法主要有两个思路；要么在每次主循环开头时，保证选择任意起始状态的概率都大于零，这种方法称之为exploring start；要么在算法运行过程中保证我们行动策略$\mu$具有足够的随机性，即能始终以一个大于零的几率访问任意可能的行动。特别地，$\forall s \in \mathcal{S}$，如果某个策略$\mu$能够保证对于每个行动的访问概率不低于$\epsilon / |\mathcal{A}(s)|$，则称这样的策略是$\epsilon$-soft的。

对于算法二第14行中定义的策略，我们称之为$\epsilon$-greedy的，它是一种$\epsilon$-soft策略。算法二中第10行是对于当前策略对应价值函数的估计，第14行是基于当前价值函数对于策略进行改进，由于探索使用的策略（第6行）和目标输出的策略（第14行）是同样的策略，因此这种方法是on-policy的。

而算法三中，探索所使用的策略$\mu$是任意固定的$\epsilon$-soft策略（第6行），比如它可以是在行动集中等概率选取行动的随机策略。而目标输出的策略$\pi$是一个关于价值函数的贪心策略，因此这种方法是off-policy的。由于行动策略与目标策略不一致，因此在更新价值函数的时候我们需要把行动策略对应的收益投影到目标函数对应的收益上。直观地来说，如果行动策略选择了某个当前目标策略大概率会选择的路径，那么对应的价值函数的改变会更多一些；反之，应该尽可能少一些地改变价值函数。这里我们使用了重要性采样（importance sampling）的技术。即目标策略对应的价值函数$V(s)$与行动策略得到的收益$G_t$应该满足如下关系。

\[V(s) = \dfrac{\sum_{t} \rho_t^{T} G_t}{\sum_{t} \rho_t^{T}}\]

其中重要性采样率（importance-sampling ratio）

\[\rho_t^{T} = \prod_{k=t}^{T-1} \dfrac{\pi(A_k|S_k)}{\mu(A_k|S_k)}\]

其中，$T$表示终止状态的时刻。算法三中的第12、13、16行所描述的就是这样的重要性采样的增量实现。

总体来说，MC方法能够通过与环境的交互来学习一个好的策略，同时它不需要对于环境的建模。其局限性在于，它只能用于回合制的任务。

时间差分方法

回顾前面的两种方法，DP方法需要直接使用对于环境的建模（即，需要使用$p(s’,r|s,a)$），而MC方法可以直接从与环境的交互经历中间来学习，它不需要知道对于环境的建模或者估计一个关于环境的模型（即，不需要使用或者估计$p(s’,r|s,a)$）。对于类似DP这样需要对环境建模的方法我们称之为model-based方法；对于类似MC这样不需要对环境建模的方法我们称之为model-free方法。同时，我们还注意到，在DP方法中，对于某个状态$s$的价值函数的估计需要使用到对于其后续状态$s’$的价值函数估计值；而在MC方法中，对于某个状态$s$的价值函数的估计来自于一整条抵达终止状态的链的实际收益，它不依赖其他状态的价值函数估计值。对于像DP这种对于一个状态价值函数估计的更新需要依赖其他状态价值函数估计的性质，我们称之为bootstrap。这里介绍的TD方法既像MC一样有model-free的特点，也像DP一样有bootstrap的性质。

回顾DP方法，DP方法在更新某个状态$S_t$的价值函数估计值的时候需要根据状态$S_t$后续所有可能状态$S_{t+1}$的价值函数估计值来更新，这种方式叫做full backup。TD方法在更新某个状态$S_t$的价值函数估计值的时候，只需要对于后续状态进行采样，使用一个后续状态$S_{t+1}$的价值函数估计值来更新即可，这种方式叫做sample backup。考虑知道了当前的状态$S_t$和目前该状态的价值函数估计值$V(S_t)$，在通过策略$\pi$行动之后到达了下一个状态$S_{t+1}$，同时取得了短期的奖励$R_{t+1}$。不难推出，相比于$V(S_t)$，$R_{t+1} + \gamma V(S_{t+1})$是一个更好的估计值，因此在每一步中，我们都把估计值$V(S_t)$往这个更好的方向更新一点，因此我们可以得到TD误差（TD error）和价值函数更新公式。

\[\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\] \[V(S_t) \leftarrow V(S_t) + \alpha \delta_t\]

与MC方法类似，TD方法也有on-policy和off-policy的版本，这里先给出他们各自的算法框图。

\[\begin{aligned} & \text{算法四：SARSA: on-policy TD Method} \\ 1\quad & \text{initialize } \forall s \in \mathcal{S}, a \in \mathcal{A}(s)\\ 2\quad & \quad Q(s, a) \leftarrow \text{arbitrary} \\ 3\quad & \quad Q(\text{terminal-state}, \cdot) \leftarrow 0 \\ 4\quad & \text{repeat for each episode:} \\ 5\quad & \quad \text{initialize } S \\ 6\quad & \quad \text{choose }A\text{ from }S\text{ using policy derived from }Q\text{ (e.g. }\epsilon\text{-greedy)} \\ 7\quad & \quad \text{repeat (for each step of episode):} \\ 8\quad & \quad \quad \text{tack action }A\text{ observe }R, S' \\ 9\quad & \quad \quad \text{choose }A'\text{ from } S' \text{ using policy derived from } Q\text{ (e.g. }\epsilon\text{-greedy)}\\ 10\quad & \quad \quad Q(S, A) \leftarrow Q(S, A) + \alpha [R + \gamma Q(S', A') - Q(S, A)] \\ 11\quad & \quad \quad S \leftarrow S', A \leftarrow A' \\ 12\quad & \quad \text{until } S \text{ is terminated} \\ \end{aligned}\] \[\begin{aligned} & \text{算法五：Q-learning: off-policy TD Method} \\ 1\quad & \text{initialize } \forall s \in \mathcal{S}, a \in \mathcal{A}(s)\\ 2\quad & \quad Q(s, a) \leftarrow \text{arbitrary} \\ 3\quad & \quad Q(\text{terminal-state}, \cdot) \leftarrow 0 \\ 4\quad & \text{repeat for each episode:} \\ 5\quad & \quad \text{initialize } S \\ 6\quad & \quad \text{choose }A\text{ from }S\text{ using policy derived from }Q\text{ (e.g. }\epsilon\text{-greedy)} \\ 7\quad & \quad \text{repeat (for each step of episode):} \\ 8\quad & \quad \quad \text{tack action }A\text{ observe }R, S' \\ 9\quad & \quad \quad \text{choose }A'\text{ from } S' \text{ using policy derived from } Q\text{ (e.g. }\epsilon\text{-greedy)}\\ 10\quad & \quad \quad Q(S, A) \leftarrow Q(S, A) + \alpha [R + \gamma \max_a Q(S', a) - Q(S, A)] \\ 11\quad & \quad \quad S \leftarrow S', A \leftarrow A' \\ 12\quad & \quad \text{until } S \text{ is terminated} \\ \end{aligned}\]

可以看到，在TD方法中，个体和环境的每产生一次交互，程序都会更新相应的价值函数。在SARSA（on-policy方法）中，目标策略和行动策略都是关于行动价值函数$Q(s,a)$的$\epsilon$-greedy策略；在Q-learning（off-policy方法）中，行动策略是关于$Q(s,a)$的$\epsilon$-greedy策略，而目标策略是关于$Q(s,a)$的greedy策略。

这里可以总结出TD方法的几个优势。首先，如同MC一样，它不需要关于环境的建模，是一种model-free的方法。其次，它在和环境的每一步交互过后都进行相应的计算，是一种完全的增量形式；与之相反的是MC方法，它需要在一个回合结束过后集中进行运算，在很多应用场景中，这是一个比较低效的方式。另外，对于有限状态的情形下（状态数目不多，以至于能够使用离散的$V(S)$或者$Q(S,A)$存储），可以证明算法的收敛性。最后，在经验上TD算法的收敛速度在很多情况下比MC和DP方法更快。

从较少的状态到庞大的状态

至此，我们对于状态价值函数和行动价值函数的表示都是针对不同的状态分别储存一个数值，并且把它们当做不同的情形来更新的。这种方式我们称之为表格方法（tabular Solution method），因为我们对于每个状态都创建了一个价值函数，在价值函数这个表格的不同格子上更新相应的价值函数。但是在很多情形下，状态可能是连续分布的，这就导致状态数目可能是无穷多的，比如一条线段上的的位置；在另外一些情形下，状态可能是通过排列组合产生的，比如100个不同颜色小球的排列，这样的情形可能产生巨大的状态数目。当我们对每个状态都采用一个格子来储存他们的价值函数时，要么遍历一遍所有的状态会消耗巨大的计算资源（比如，DP算法中需要对于某个状态的后续所有可能的状态遍历），要么在很长的计算时间内，总有大量的状态一次都不能被更新到（比如，MC或者TD算法中虽然并不要求每次迭代遍历所有的状态，但是有些状态一次都不能被访问到会导致算法性能大幅下降）。

当我们遇到无穷或者庞大的状态集的时候，我们需要采取近似方法（approximate Solution method）。我们通常使用一组参数来控制相应的状态价值函数（如果是行动状态函数也是类似的处理方法），我们把状态价值函数$v(s)$写成$v (s, \mathbf{\theta})$的形式，它的具体形式可以根据不同任务而不同，比如最简单的也是我们下面讨论中默认的一种形式——线性近似（linear approximation）$v(s, \mathbf{\theta}) = \mathbf{\theta}^T \mathbf{s}$，其中$\mathbf{\theta}$和$\mathbf{s}$是维度相同的向量，最常见的$\mathbf{s}$可以使one-hot形式的向量，表示该状态处于某个状态组中。因此当我们要更新状态价值函数的估计值时，我们不再对于某一个格子上的数值直接进行更新，而是对于参数$\mathbf{\theta}$进行更新

\[\mathbf{\theta}_{t+1} = \mathbf{\theta}_t + \alpha [G_t - v(S_t, \mathbf{\theta}_t)] \nabla_\theta v(S_t, \mathbf{\theta}_t)\]

当然，这样的近似价值函数还可以使用更为复杂的形式来表示，比如使用神经网络等。

TD($\lambda$)算法

回顾前面的TD和MC方法，在TD方法中，每次都把当前的状态价值函数都往一个更为合理的状态价值函数估计值$G_t^{(0)} = R_{t+1} + \gamma v(S_{t+1}, \mathbf{\theta})$上更新；在MC方法中，我们每次实际上是将状态价值函数估计值往$G_t^{(T-t)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma^{T-t} R_T$上更新。我们其实可以定义$n$步的TD算法，使得其目标收益估计为

\[G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma^n v(S_{t+n}, \mathbf{\theta}), 0\le t\le T-n\]

实际上对于$G_t^{(n)}$的任意归一化的加权组合都能够形成可行复合收益估计，比如$\frac{1}{4}G_t^{(1)} + \frac{3}{4}G_t^{(2)}$。这里我们定义一种特殊的复合收益估计，称之为$\lambda$-收益（$\lambda$-return）

\[G_t^\lambda = (1-\lambda) \sum_{n=1}^\infty \lambda^{n-1} G_t^{(n)}\]

其中$0\le\lambda\le 1$，根据$\lambda$取值的不同，$\lambda$-收益对应的实际上是从MC方法到前述TD方法（也称TD(0)方法）的过渡。当$\lambda = 0$时，$\lambda$-收益对应的就是一步的TD方法；当$\lambda = 1$时，$\lambda$-收益对应的就是MC方法。

下面我们写出使用$\lambda$-收益对应的TD($\lambda$)算法。这里是对于某个给定的策略$\pi$来计算相应的价值函数，这种问题称之为预测问题（prediction problem）；如果我们的目标是要求出最优策略$\pi^*$以及相应的价值函数，那么这种问题称之为控制问题（control problem）。

\[\begin{aligned} & \text{算法六：TD(}\lambda \text{): TD prediction using } \lambda \text{ return} \\ 1\quad & \text{input: the policy } \pi \text{ to be evaluated}\\ 1\quad & \text{initialize value function weights } \mathbf{\theta} \text{ arbitrarily (e.g. all zeros)}\\ 2\quad & \text{repeat (for each episode)} \\ 4\quad & \quad \text{initialize state} \\ 5\quad & \quad \mathbf{e} \leftarrow \mathbf{0} \\ 5\quad & \quad V_{old} \leftarrow 0 \\ 7\quad & \quad \text{repeat (for each step of episode):} \\ 8\quad & \quad \quad \text{choose }A\text{ follow } \pi \\ 9\quad & \quad \quad \text{take action }A\text{ observe } R, \mathbf{s}' \text{(feature vector of the next state)}\\ 11\quad & \quad \quad V \leftarrow \mathbf{\theta}^T \mathbf{s} \\ 11\quad & \quad \quad V' \leftarrow \mathbf{\theta}^T \mathbf{s}' \\ 11\quad & \quad \quad \delta \leftarrow R+\gamma V' - V\\ 11\quad & \quad \quad \mathbf{e} \leftarrow \gamma\lambda \mathbf{e} + (1-\alpha \gamma \lambda \mathbf{e}^T \mathbf{s}) \mathbf{e}\\ 11\quad & \quad \quad \mathbf{\theta} \leftarrow \mathbf{\theta} + \alpha (\delta + V - V_{old}) \mathbf{e} - \alpha(V- V_{old}) \mathbf{s}\\ 11\quad & \quad \quad V_{old} \leftarrow V'\\ 11\quad & \quad \quad \mathbf{s} \leftarrow \mathbf{s}'\\ 12\quad & \quad \text{until arrive at a terminal state} \\ \end{aligned}\]

其中这里应用到了一种称之为eligibility trace的技术，通过这种技术，可以将运算量从集中地在每次回合结束时进行变为分散在每一步之中进行。特别地，$\mathbf{e}$也称作eligibility trace。大体上来说，它是与状态特征向量$\mathbf{s}$维度相同的向量，它记录了历史中每一步的所经历的状态的累积，通过更新它，可以使我们能够先记录走过的路径，在最后得到相应的收益之后，再往正确的方向更新。

类似地，相应的使用$\lambda$收益的控制问题可以基于算法五和算法六得到。

参考文献

[1] Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. Vol. 1. No. 1. Cambridge: MIT press, 1998.

[2] Watkins, Christopher JCH, and Peter Dayan. “Q-learning.” Machine learning 8.3-4 (1992): 279-292.

[3] Rummery, Gavin A., and Mahesan Niranjan. On-line Q-learning using connectionist systems. Vol. 37. University of Cambridge, Department of Engineering, 1994.